「指示を受けた人のミスを減らす指示」の出し方
これは、自分だけの問題ではなく、指示を出すときにも重要な考え方です。簡単にできるように工夫をして指示してあげれば、指示された側でミスが減るのです。
AさんとBさんが100m離れたところから向かい合って歩き始めます。
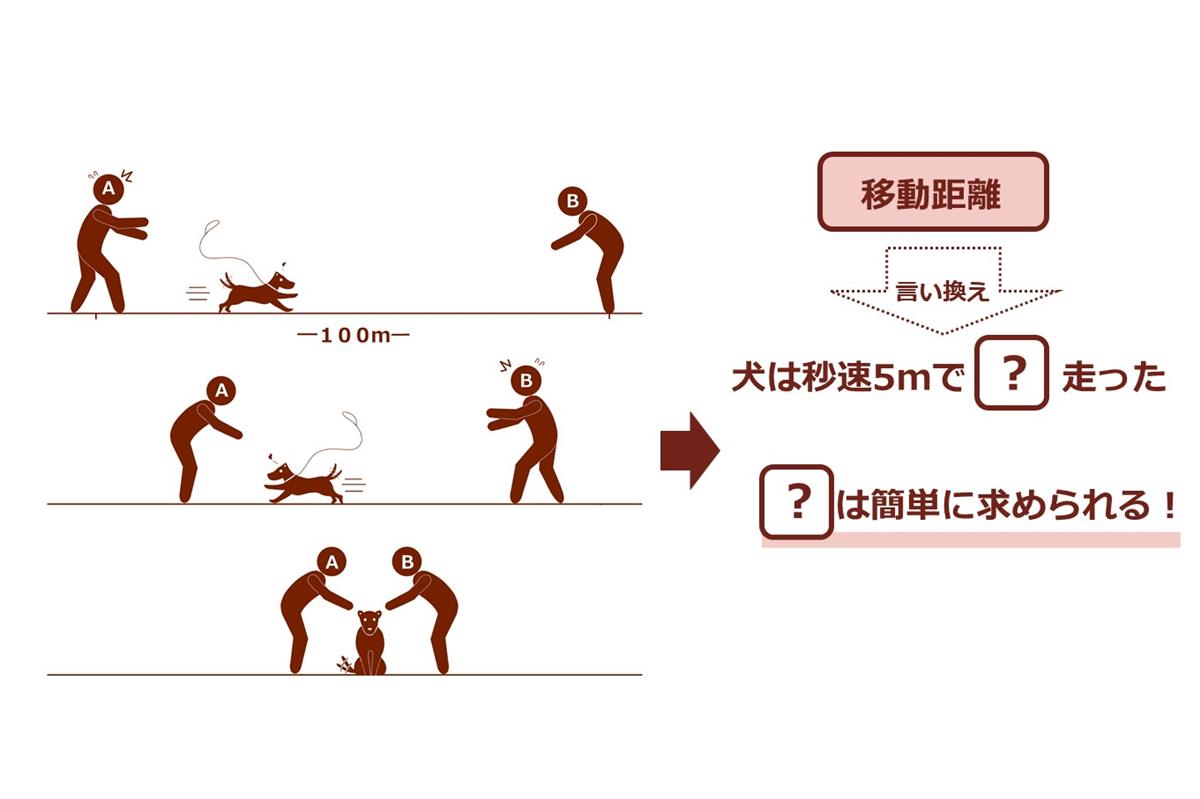
Aさんは秒速3m、Bさんは秒速2mで歩きます。Aさんは犬を連れていて、歩き始めると同時にリ-ドを離します。犬はそこからBさんに会えるまで走っていき、Bさんに会うとすぐにAさんの方に引き返していきます。そして、Aさんのところまで戻ると、再びすぐにBさんの方に向かってかけていきます。2人のことが大好きな犬は2人の間を秒速5mで往復し続けます。
AさんとBさんが出会うまでに犬は何m走るでしょうか?
これも小学生の問題です。下のイラストのように考えると、犬の移動距離を測定するのはすごく複雑そうですね。しかし、移動距離=速さ×移動時間です。よって「移動距離を測定する」ことは、「移動時間を測定する」ことと同じ意味を持つのです。移動距離を捉えるのは難しそうに見えますが、移動時間は簡単です。
これは、2人が出会うまでの時間ですから、「100m÷(3+2)=20秒後」です。よって犬は「5×20=100m」走ることになります。
これも、「移動距離」という難しいものを、「移動時間」という求めやすいものにすり替えることで簡単に求めることができるという一例です。
最後は社会人向け算数・数学講座でもよく取り上げられる例題をご紹介します。
100人にアンケ-トをとりました。
スマホを持っている人は80人、タブレットを持っている人は60人、パソコンを持っている人は90人、どれも持っていない人は2人いました。
パソコンを持たずにスマホ、タブレットで済ませている人は何人いますか?
「パソコンをもたずに」というヒント文を挿入してみました。「スマホ、タブレットで済ませている人は何人いますか?」と質問するよりも答えを出しやすくなります。
パソコンを持っている人が90人なので、「パソコンを持っていない人」は10人です。この10人が、パソコンをもたずに済ませている人です。この中には「何も持っていない2人」が含まれていますね。よって、「10-2=8人」が、「パソコンをもっていないが、何も持っていないわけではない人」で、これが答えになります。
「パソコンを持っている人」という情報から簡単に求められる「パソコンを持っていない人」を考えることがポイントでした。
「算数の姿勢」でミスを減らす
「複雑な作業を複雑なまま丁寧にやる」のは美徳かもしれませんが、ミスの危険が付きまといます。同じ意味・結果を出せる別の簡単な考え方はないかと探る姿勢は算数の基本です。算数・数学が得意な人はめんどくさがりが多いというのは通説です。みなさんもぜひ、「良質なめんどくさがり」になってください。
【今日から使えるロジカルシンキング】は子供向けにロジカルシンキングのスキルを身につける講座やワークショップを開講する学習塾「ロジム」の塾長・苅野進さんがビジネスパーソンのみなさんにロジカルシンキングの基本を伝える連載です。アーカイブはこちら